Compact Low Voltage Free Space Electro-Optical Modulators: Phase or Intensity
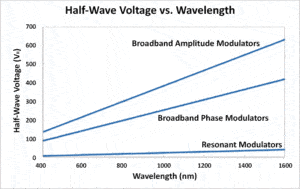 Our Electro-optic modulators are based on a special crystal that has less piezo-effect and low charge migration than the traditional Mg doped Lithium Niobate crystals, resulting in clean response with less ringing, more efficient with less power consumption, the ability to work at shorter wavelength and higher optical power. We produce two versions: resonant and direct driving. Both modify the phase, polarization or amplitude of a free-space laser: The resonant modulator drastically reduces driving voltage so that it can be driven by a laboratory function generator. Each device uniquely has three fixed resonance frequencies of 1MHz, 15MHz, and 30MHz that can be manually select via a toggle switch. Our resonance electro-optic modulator is a cost effective and convenient device for testing applications. Custom frequencies up to 100MHz are also available. Another version is direct driving modulator that can be operated from DC to high frequencies. However, it needs a high voltage driver which determines its performance. We produce a high-voltage driver. Customer can use drivers from other manufacturers.
Our Electro-optic modulators are based on a special crystal that has less piezo-effect and low charge migration than the traditional Mg doped Lithium Niobate crystals, resulting in clean response with less ringing, more efficient with less power consumption, the ability to work at shorter wavelength and higher optical power. We produce two versions: resonant and direct driving. Both modify the phase, polarization or amplitude of a free-space laser: The resonant modulator drastically reduces driving voltage so that it can be driven by a laboratory function generator. Each device uniquely has three fixed resonance frequencies of 1MHz, 15MHz, and 30MHz that can be manually select via a toggle switch. Our resonance electro-optic modulator is a cost effective and convenient device for testing applications. Custom frequencies up to 100MHz are also available. Another version is direct driving modulator that can be operated from DC to high frequencies. However, it needs a high voltage driver which determines its performance. We produce a high-voltage driver. Customer can use drivers from other manufacturers.
- 3 mm Aperture
- Wide Operation Wavelength 450 to 1550 nm
- High Optical Power Handling
- Low Driving Voltage ~12V (resonance)
- One Device with Three Frequencies To Select (1, 15, 30MHz)
- High Repetition Rate Up to 100MHz (Resonance)
- Broadband DC to 1MHz (non-Resonance)
- Fiber Coupled Available
- Customization Available
-
 This product has multiple variants. The options may be chosen on the product page
This product has multiple variants. The options may be chosen on the product pageAmplitude/Phaser Electro-Optical Modulator – No Resonance
3mm aperture, 450~1550nm, DC to 1MHz, need high voltage driver
$2037+
SKU: EOMN
$2,037 – $7,887 -
 This product has multiple variants. The options may be chosen on the product page
This product has multiple variants. The options may be chosen on the product pageAmplitude/Phaser Electro-Optical Modulator – Resonance
3mm aperture, 450~1550nm, fixed frequency at 1-20 MHz
$2548+
SKU: FEOM
$2,548 – $9,080 -
 This product has multiple variants. The options may be chosen on the product page
This product has multiple variants. The options may be chosen on the product pageGHz Phase Modulators – Resonance
1-3.05 GHz, temperature control option
$4859+
SKU: GHZM
$4,859 -
 This product has multiple variants. The options may be chosen on the product page
This product has multiple variants. The options may be chosen on the product pageHigh Voltage Electro-Optical Modulator/Switch Driver
up to 400V
$2456+
SKU: HVED
$2,456 – $4,159

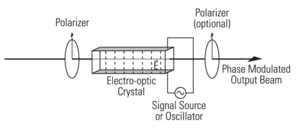
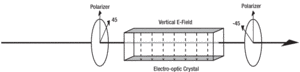 along the two crystal directions to a different degree, thereby changing the retardation of the effective waveplate.
along the two crystal directions to a different degree, thereby changing the retardation of the effective waveplate.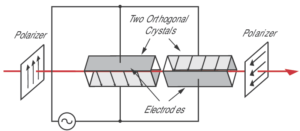 temperature. Thermal drift limits the usefulness of a phase modulator, which is typically made out of a single crystal.
temperature. Thermal drift limits the usefulness of a phase modulator, which is typically made out of a single crystal.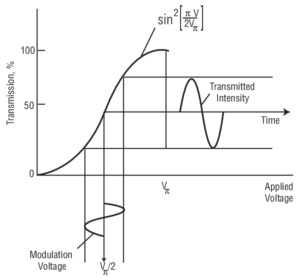 modulation voltages by biasing the modulator at the 50% transmission point, either with a quarter-wave plate or by applying a DC voltage to the modulator.
modulation voltages by biasing the modulator at the 50% transmission point, either with a quarter-wave plate or by applying a DC voltage to the modulator.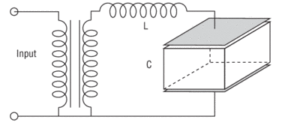 high-frequency modulators (to 250 MHz) find applications in mode-locking (AM and FM), laser stabilization, phase-sensitive detection, and pump-probe detection schemes. Modulators with frequencies to 10 GHz find applications in FM spectroscopy, laser stabilization, and laser linewidth-broadening experiments.
high-frequency modulators (to 250 MHz) find applications in mode-locking (AM and FM), laser stabilization, phase-sensitive detection, and pump-probe detection schemes. Modulators with frequencies to 10 GHz find applications in FM spectroscopy, laser stabilization, and laser linewidth-broadening experiments.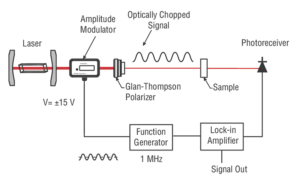
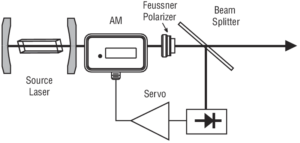 the laser intensity which the servo uses to adjust the transmission of the amplitude modulator. An important consideration in this application is the nonlinear response of the modulator. The changing slope of the modulator’s response to input voltage leads to a change in the closed-loop transfer function which could destabilize the feedback loop. An amplitude modulator can be used to reduce the amplitude fluctuations.
the laser intensity which the servo uses to adjust the transmission of the amplitude modulator. An important consideration in this application is the nonlinear response of the modulator. The changing slope of the modulator’s response to input voltage leads to a change in the closed-loop transfer function which could destabilize the feedback loop. An amplitude modulator can be used to reduce the amplitude fluctuations.